이번 학기로 생명공학과 대학생으로서 들어야 하는 수업은 다 듣게 되는데, 그 수업 중 하나가 생물 물리학이다. 지난 학기에 생체 유체역학에 데인 적이 있어서 ('생체 유체역학'이 아니라 생체 '유체역학'이었던 과목이라 물리과가 된 기분이었다ㅠㅠ) 정말 안끌렸지만 전공 필수라 눈물을 머금고 신청했다.
개인적으로 물리를 싫어하진 않고, 또 아직까진 들을만 해서 생각한 것보다 고통스럽진 않다. 지금 배우고 있는 내용은 엔트로피의 통계역학적 해석인데, 말은 거창하지만 엔트로피를 통계적 시각으로 접근하는 것이라 잘 모르는 화학이나 열역학적인 내용이 없어서 좋다. 좋다는게 잘 안다는 의미는 아니지만...ㅎㅎ
공대 다니면서 언젠가 한번은 들었던 '엔트로피'인데 잘 모른다는게 조금 부끄럽기도 하고, 수업내용이기도 해서, 조금 이해가는 방식이 나왔을 때 정리하고 가면 좋을 것 같아 블로그에 남겨보려한다. 오개념과 이유 모를 근사가 난무할 수 있지만 뭐...배우는 중이고 무엇보다 내 블로그니까 괜찮을듯!
Entropy (엔트로피)
Entropy is a measure of the number of different ways of rearranging the system. In particular, the entropy of a closed system provides a measure of the number of different microscopic ways that we can realize a given observed macroscopic state, and can be written as $$S = k_Bln\Omega$$
(Physical Biology of The Cell second edition, Rob Phillips et al.)
위의 문장은 위키피디아에 정의된 통계역학적 엔트로피의 정의와 동치이다. 즉, 엔트로피 S는 주어진 거시적 상태 (macrostate) 에 대응하는 미시적 상태 (microstate)의 수($\Omega$)의 자연로그 * Boltzmann constant 로 생각할 수 있다.
일단은 엔트로피는 주어진 거시적 상태 (macrostate)에 대응하는 미시적 상태 (microstate)의 수이다. 그럼 '거시적 상태에 대응하는 미시적 상태'란 무슨 말일까?
거시적 상태는 정의하기 나름인데, 시스템의 temperature, pressure, volume, density를 특정한 하나의 상태 (state)로, 디폴트 값만 정해준 상태 정도로 이해하면 될 것 같다. 미시적 상태는 그 거시적 상태에 포함되는 모든 상태를 의미한다. 예를 들어 같은 조건의 solution이 있고, 10개의 molecules가 들어있으며, 이 solution을 반으로 가르는 임의의 선이 있다고 하자. 이 때 macrostate 1을 molecules가 그 임의의 선을 기준으로 반반으로 분배돼있는 상태이고, macrostate 2를 molecules가 그 임의의 선을 기준으로 10:0으로 분배돼있는 상태라고 정의해보자.
그렇다면, macrostate 1과 macrostate 2에 대응하는 microstate는 각각 몇개일까?
경우의 수를 생각하면 각각의 macrostate에 대응하는 microstate는 10C5, 10C10개이다. 이 microstate의 수를 multiplicity라 하고 기호로는 $\Omega$로 나타낸다. 따라서 macrostate 1 의 multiplicity는 10C5이고, macrostate 2의 multiplicity는 10C10이다. 그러므로 macrostate 1의 entropy S는 $k_{B}\ln{10C5}$이고 macrostate 2의 S는 $k_{B}\ln{10C10}$이다.
이러한 엔트로피 정의는 equilibrium state를 이해하는데도 도움이 된다.
엔트로피와 equilibrium state
Free energy G is,
$$G = H - TS$$
...the equilibrium state of a system is that choice out of all states available to the system that minimizes the free energy
(Physical Biology of The Cell second edition, Rob Phillips et al.)
즉, 평형상태는 여러 상태 중 free energy를 최소로 하는 상태를 말한다. free energy 식에 따르면 free energy가 최소가 되기 위해선 S의 contribution이 높아져야한다. S의 contribution이 높다는 것은 $\Omega$의 값이 크다는 의미이고 (자연로그는 단조증가하므로) 이전의 예 중에선 macrostate 1이 macrostate 2보다 평형상태에 가깝다.
신기하게도, 높은 엔트로피의 macrostate가 선호되는 것은 그 macrostate의 확률과도 관련이 있다. 이전의 예로 계속 설명하자면, 모든 microstate의 경우의 수는 2^10이다. 그리고 macrostate 1, macrostate 2 각각의 경우의 수는 각각의 mutiplicit였으므로 확률을 계산하면 macrostate 1이 발견될 확률이 macrostate 2가 발견될 확률보다 더 높다는 의미이다. 따라서 엔트로피가 증가하는 이유는 증가하는 방향에 있는 macrostate의 확률이 높기 때문이라 할 수 있다.
방금 언급한 macrostate의 확률은 multiplicity의 영향을 받기 때문에, molecule의 수가 커지면 커질수록 극단적 상태 (eg. macrostate 2)와 평형상태 (eg. macrostate 1)의 확률 차이는 상당해진다. 아래의 figure를 보면 어떤 의미인지 쉽게 이해할 수 있다.
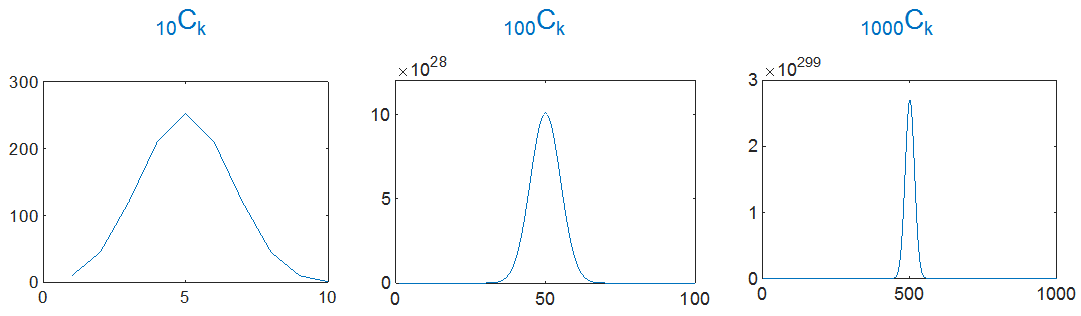
각 그래프의 양 끝이 극단적 상태이고, 중간이 평형상태 (혹은 평형상태와 제일 가까운 상태)이다. 그래프에서 알 수 있듯, molecule의 수가 10일때는 극단적 상태와 평형상태의 차이가 약 250배 가량이지만 molecule의 수가 1000일때는 그 차이가 말도 안되게 크다. 또, molecule의 수가 커질수록 첨도가 커져 molecule 수의 감소량 혹은 증가량이 조금만 되어도 확률이 급격히 떨어짐을 알 수 있다.
사실, 지금까지 언급한 예시는 특정한 경우일 뿐이고, macrostate의 확률은 Boltzmann factor를 사용하는 것이 정확하다. Boltzmann factor에 대한 이야기는 다음 글에서 다루도록 하고, 이번 글은 엔트로피와 소수성의 관계에 대해 추가로 알아보고 마무리 하려한다.
엔트로피와 소수성 (hydrophobicity)
소수성(hydrophobicity)은 비극성 물질에서 나타나는 경향으로 물 분자에서 배제되어 응집되는 것을 말한다. 'hydrophobic'이라는 단어는 ‘물을 두려워하는’이라는 의미를 담고 있는데 소수성 물질이 친수성 액체 내에 있을 때는 마치 물을 두려워하듯 소수성 결합을 증가시키면서 소수성 물질들이 응집한다. 이는 세포막 및 소포 형성, 단백질 접힘, 비극성 지질 환경 속으로 단백질 삽입 등의 효과를 나타낸다.[네이버 지식백과] 소수성 [hydrophobicity] (생화학백과)
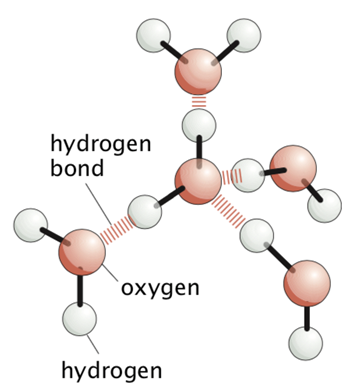
물 분자는 위 그림처럼 수소결합을 형성 할 수 있다. 이 예에서 쓰인 수소 결합체가 만드는 4면체의 구조에서, 중앙의 물 분자의 orientation은 수소 원자의 orientation에 따라 6가지가 가능하다 해보자. 즉, 4면체라는 하나의 macrostate에 6개의 microstate가 대응되는 셈이다.

이 때, 만약 소수성 물질이 들어와 수소 결합체의 물 분자 중 하나의 자리를 차지하게 되면 (예를 들어 오른쪽 하단 물분자의 자리를 대체하게 되면) 중앙의 물 분자의 orientation은 줄어들게 된다. 예시에선 위의 세 가지 경우만 가능하게 되어 multiplicity가 3이 돼버린다. 결과적으로 엔트로피 차이는

가 되고, free energy의 차이는

가 되어 양수가 돼 비자발적 반응이 된다. 또한, 이 계산은 물 분자 하나에 대한 계산이므로, 소수성 물질에 n개의 물분자가 인접해있다하면 free energy의 차이는

가 돼 그 크기가 더욱 커지게 된다. 수가 정확하지 않을 수 있지만 그 경향은 수가 어떻든 유지된다.
그렇기 때문에 소수성 물질이 친수성 액체에 들어가게 되면 물질끼리 응집해서 표면적을 줄여 (인접하는 물분자의 갯수 n을 줄여)

이 작아지게끔 하고, 그 결과 세포막 및 소포 형성, 단백질 접힘, 비극성 지질 환경 속으로 단백질 삽입 등의 효과가나타나게되는 것이다.
'생명공학' 카테고리의 다른 글
| 로그 스케일 (0) | 2021.04.26 |
|---|---|
| [공대생이라면 한 번쯤 들어보는... 1] 엔트로피 (2) (0) | 2021.04.08 |
| DNA databases are too white, so genetics doesn’t help everyone. How do we fix that? (2) (0) | 2021.03.07 |
| DNA databases are too white, so genetics doesn’t help everyone. How do we fix that? (1) (0) | 2021.03.06 |
| Genomics VS Bioinformatics (0) | 2021.01.14 |

